Алгоритм Евклида в Pascal
Может Pascal сегодня не так популярен, но он отлично подходит в образовательных целях. Именно на его примере и будет показан один из основных алгоритмов для криптографии, а именно алгоритм Евклида
Что такое алгоритм Евклида
Алгоритм Евклида является самым быстрым способом найти наибольший общий делитель (НОД) двух чисел. В отличие от обычного перебора, алгоритм Евклида ищет ответ в десятки раз быстрее.
Немного об истории. Евклид был математиком, который родился в 325 году до н.э. Алгоритм Евклида был опубликован в его трудах «начало», где, кстати, и была выдвинута теория о бесконечном множестве простых чисел.
Сфера применения алгоритма
Для программистов НОД – это не только знакомая тема из начальной школы. Принципы поиска делителя заложены в криптографические методышифрования, а именно в тип шифрования RSA.
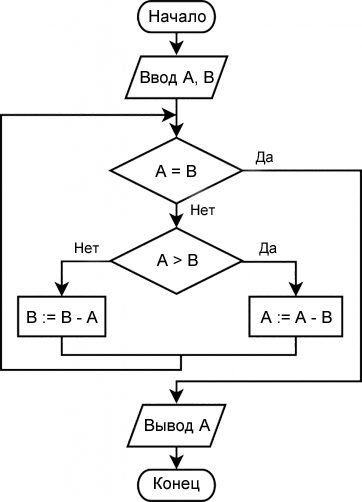
Алгоритм Евклида с вычитанием
Давайте рассмотрим алгоритм на примере. Нам необходимо найти наибольший общий делитель у чисел 68 и 323:
A = 68
B = 3231. A>B – Нет, тогда b = 323 – 68= 255;
2. A>B – Нет, тогда b = 255 – 68 = 187;
3. A>B – Нет, тогда b = 187 – 68 = 119;
4. A>B – Нет, тогда b = 119 – 68 = 51;
5. A>B – Да, тогда a = 68 – 51 = 17;
6. A>B – Нет, тогда b = 51 – 17 = 34;
7. A > B – Нет, тогда b = 34 – 17 = 17
8. A = B, Да, тогда НОД = A= 17Ответ: НОД = 17
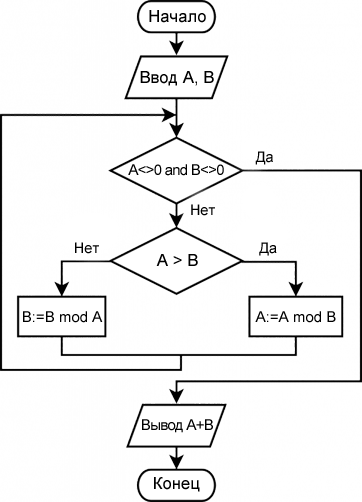
Алгоритм Евклида с делением
Проверим на том же примере:
A = 68
B = 3231. A>B – нет, тогда B = 323 по модулю 68 = 51;
2. A > B – Да, тогда A = 68 по модулю 51 = 17;
3. A>B – Нет, тогда B = 51 по модулю 17 = 0;
4. Aи B = 0, тогда ответ равен 17 + 0 = 17.Ответ: НОД(68,323) = 17
Этот метод намного быстрее первого.
Сравнение с методом перебора
Теперь найдем НОД самым примитивным способом – перебором. Наши числа – 68, 323. Неожиданно?
Чтобы быть точно уверенными, что наш метод работает, нам необходимо проверить 68 операций. А Евклид справился всего за 5. Вот и разница. Никто не пользуется методом перебора.
Реализация на Pascal
Осталось выполнить код в паскале:
vara, b: integer;
begin
write(‘a = ‘);
readln(a);
write(‘b = ‘);
readln(b);
while a <> b do
if a > b then
a := a – b
else
b := b — a; writeln(‘NOD = ‘, a);
end.
Заключение
Алгоритм Евклида – самый практичный способ нахождения наибольшего общего делителя. Его нужно знать каждому, кто желает выучить основы алгоритмов в программировании.